
Студенческий меридиан
Выпуском журнала занимался коллектив журналистов, литераторов, художников, фотографов. Мы готовим рассказ о коллегах и об их ярких, заметных публикациях.
А сейчас назову тех, кто оформлял СтМ с 1990-х до 2013-го.
Главный художник
мастер компьютерного дизайна
и фотограф Игорь Яковлев.
Большая часть обложек и фоторепортажей – творческая работа Игоря Яковлева.
Надеюсь, что нам удастся представить Вам увлекательную историю создания и деятельности СтМ.
Юрий Ростовцев, гл. редактор
«Студенческого меридиана», журнала,
которому я с удовольствием служил
с 1977 по 2013 годы.
Номер 02, 2012
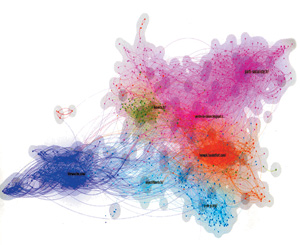
Скрытые структуры галактики интернет
 |
| Граф, представляющий 1052 политических блога во Франции в 2011 года. Размер точек указывает на влияние сайтов. Арки показывают гипертекстовые связи, связывающие их, а цвет – политические семьи. Сайты с большим количеством связей в общем близки. |
 |
| Изображение сети интернет с ее миллионами компьютеров. Узлы есть адреса IP (крупный план справа), а цвет соответствует именам доменов (com, org). Длина связей этих узлов зависит от времени, которое тратит информация на прохождение между ними (данные 2005 г.). |
Что общего между Кенигсбергом XVII века и социальной сетью «Фейсбук» – современной звездой веба? И то, и другое в разных масштабах иллюстрирует особую математическую теорию, развитую в ХХ веке: теорию графов.
На бумаге нет ничего более очевидного, чем граф. Это – комплекс точек (их называют еще «узлами»), объединенных связями (или ребрами). Для Кенигсберга это кварталы и их связи, его семь мостов. Для социальных сетей узлы являются личными страницами и связями, объяснениями в «дружбе». Электрическая сеть, генеалогическое древо или маршрут коммивояжера – другие примеры графов.
На основе этого простого определения математики сформулировали множество вопросов. Каков самый короткий путь между двумя точками? Каковы все способы их связи? Есть ли изолированные точки или очень плотные зоны? Можно ли обнаружить простые правила позади этого множества узлов и связей?
Набор вопросов, который задал Леонард Эйлер в 1759 году по поводу мостов Кенигсберга – он еще не использовал термин граф, – можно ли пройти по ним всем за один раз и вернуться в точку старта? Ответ: нет. Сегодня математики и специалисты по информатике пытаются исследовать гигантские графы, рожденные в вебе «Фейсбуком» (и его 700 миллионами узлов), и другие сети попарно. Их цель «идентифицировать и «картографировать» «сообщества». В 2008 году был предложен алгоритм, наиболее эффективный для подобных расчетов.
Это один из последних примеров сложной связи между вебом и графами. Новые объекты вдохновляют ученых. Эти работы привели к рождению «Гугла». Чтобы найти информацию, его поисковик «классифицирует» страницы веба (это узлы графа – 30 миллиардов точек) в зависимости от правил, основанных на гипертекстовых связях, соединяющих одну страницу с другой. Страница, «получающая» больше связей (иными словами – цитируется чаще и другими сайтами), будет иметь лучший счет, чем страница, которую никто не смотрит.
По мере роста этого нового объекта веба математики, информатики и физики начали изучать его, как любой естественный объект. В конце прошлого и начале этого века они натолкнулись на удивительные свойства сети – она не такая гигантская, как представлялось! Ее возможно пройти менее чем за двадцать «кликов» из конца в конец по гипертекстовым связям. Это близко к выводам социолога Стенли Миллгрэма, который в 1967 году определил по почтовым посланиям: за шесть «ударов» письмо можно послать кому угодно, даже не зная адреса.
Другая занимательная особенность этой сети – отсутствие понятия «среднее». Нельзя сказать, что в среднем сайт имеет Х связей или абонент социальной сети имеет Х друзей. Есть огромное количество сайтов с малым количеством связей и меньшинство – с огромным их количеством.
Иными словами, математический закон, занимающийся количеством связей и узлов, является не законом Гаусса (кривая колокола), а законом степени. Первый описывает отметки в классе (в среднем мало учеников имеют 5 и 1). Второй случай: распределение богатств в обществе: 20% обладают 80% богатств.
И последнее свойство, стимулирующее исследователей, имеет и доходное применение: структура сообщества. Веб наполнен «маленькими мирами», плотными зонами, чьи точки тесно связаны друг с другом и почти не связаны с остальной частью сети. Пословица «друзья моих друзей – мои друзья» работает, но не продолжается до бесконечности. Проблема состоит в использовании инструментов для обнаружения этих агрегатов, этих сообществ или этих «кликов». Методы, подходящие для маленьких графов, не работают с объектами из миллионов точек. И надо определить критерии, чтобы сказать – та или иная группа является сообществом.
Зачем искать эти агрегаты? Для обеспечения безопасности связей в информационной сети из нескольких машин полезно знать уязвимые точки, чтобы изолировать их в случае атаки. Разведслужбы также заинтересованы в идентификации особых групп (террористы) и наблюдении за ними. Рекламщики заинтересованы в идентификации этих сообществ по интересам, чтобы уточнить адрес своих посланий или воздействовать на их «лидеров». Создаются стартапы для картографирования и наблюдения за блогами, социальными сетями, сайтами микроблогинга... для зондирования или рекламщиков. Они могут узнать в реальном времени, кто о чем говорит, с каким настроением (положительным или отрицательным) и как распространяются послания.
Научный вызов – наблюдение за тем, как эти структуры меняются во времени: какое сообщество создается, распадается, сливается? Пока это еще лабораторная проблема.
Многие уже задумываются о рисках, связанных с этими новыми инструментами. Они не должны нарушать частную жизнь, а быть инструментами публичными.
К началу ^

